Trees

A special type of graph, trees excel at storing data hierarchically and are commonly used as a means of testing your knowledge of recursion during coding interviews.

Interesting fact: unlike their botanical counterparts, these digital perennials sport but a single, unique root.

Tree A data structure that consists of nodes, each with some value and pointers to child-nodes, which recursively form subtrees in the tree. The first node in a tree is referred to as the root of the tree, while the nodes at the bottom of a tree (the nodes with no child-nodes) are referred to as leaf nodes or simply leaves. The paths between the root of a tree and its leaves are called branches, and the height of a tree is the length of its longest branch. The depth of a tree node is its distance from its tree's root, this is also known as the node's level in the tree.

A tree is effectively a graph that's connected, directed, and acyclic, that has an explicit root node, and whose nodes all have a single parent (except for the root node, which effectively has no parent). Note that in most implementations of trees, tree nodes don't have a pointer to their parent, but they can if desired.

There are many types of trees and tree-like structures, including binary trees, heaps, and tries.

Binary Tree

A tree whose nodes have up to two child-nodes. The structure of a binary tree is such that many of its operations have a logarithmic time complexity, making the binary tree an incredibly attractive and commonly used data structure.

K-ary Tree

A tree whose nodes have up to k child-nodes. A binary tree is a k-ary tree where k == 2

Perfect Binary Tree

A binary tree whose interior nodes all have two child-nodes and whose leaf nodes all have the same depth.

Example:

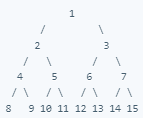
Complete Binary Tree

A binarry tree that's almost perfect; its interior nodes all have two child-nodes, but its leaf nodes don't necessarily all have the same depth. Furthermore, the nodes in the last level of a complete binary tree are as far left as possible.

Example:

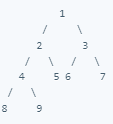
Conversely, the following binary tree isn't complete, because the nodes in its last level aren't as far left as possible:

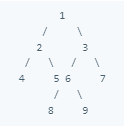
Balanced Binarry Tree

A binary tree whose nodes all have left and right subtrees whose heights differ by no more than 1.

A balanced binary tree is such that thae logarithmic time complexity of its operations is maintained.

For example, inserting a node at the bottom of the following imbalanced binary tree's left subtree would clearly not be a logarithmic-time operation, since it would involve traersing though most of the tree's nodes:

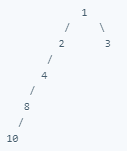
The following is and example of the balanced binary tree.

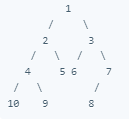
Full Binary Tree

A binary tree whose nodes all have either two chid-nodes or zero child-nodes.

Example: